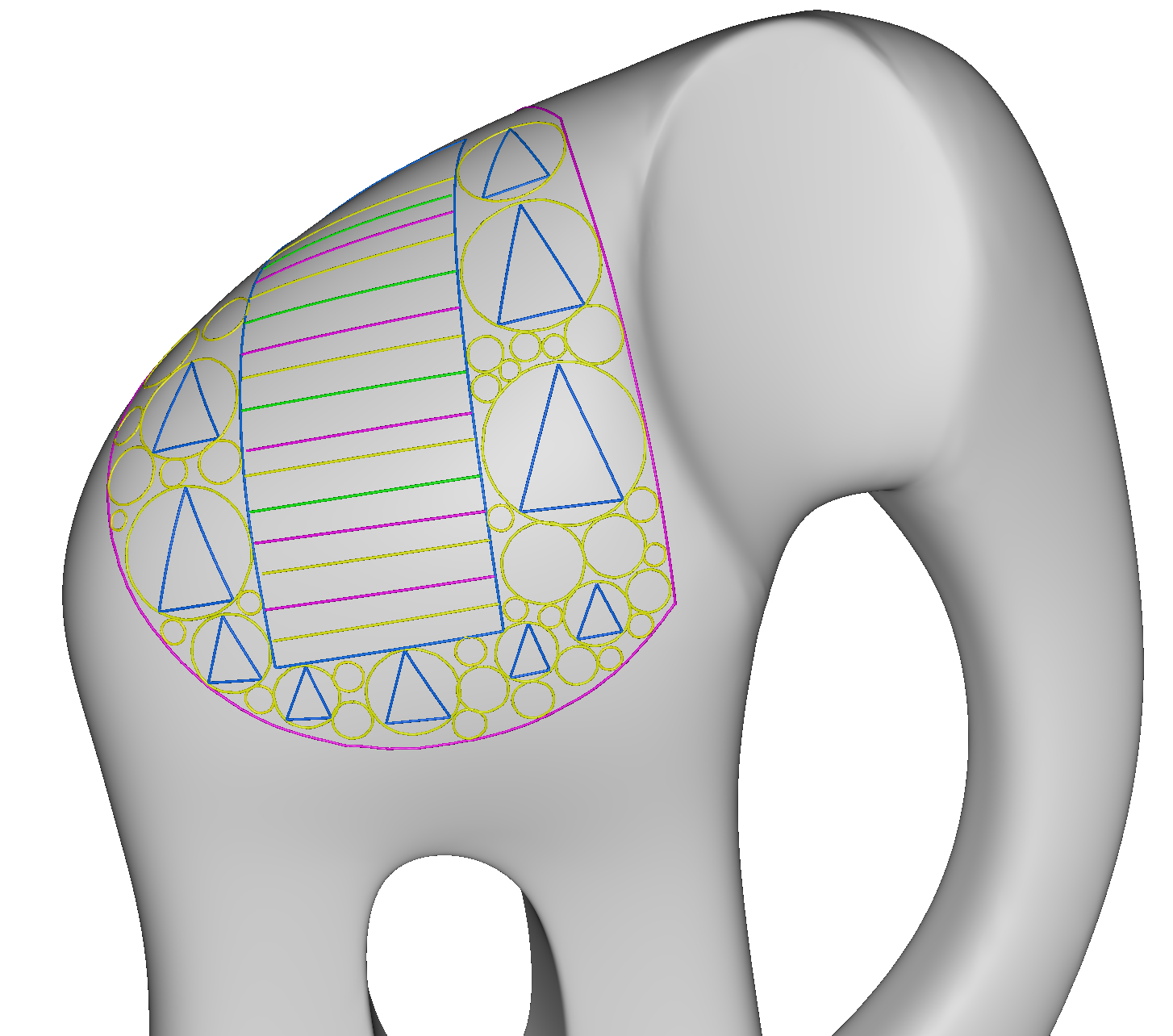
We discuss how classical straightedge and compass constructions can be ported to manifold surfaces under the geodesic metric. After defining the equivalent tools in the manifold domain, we analyze the most common constructions and show what happens when trying to port them to surfaces. Most such constructions fail, because the geometric properties on which they rely no longer hold under the geodesic metric. We devise some alternative constructions that guarantee at least some of the properties of their Euclidean counterpart; while we show that it is usually impossible to guarantee all properties together. Some constructions remain still unsolved, unless additional tools are used, which violate the constraints of the straightedge and compass framework since they take explicit distance measures. We integrate our constructions in the context of a prototype system that supports the interactive drawing of vector primitives on a surface represented with a high-resolution mesh.

(paper)              

          @inproceedings {MP21-STAG
            booktitle = {Smart Tools and Apps for Graphics - Eurographics Italian Chapter Conference},
            editor = {Frosini, Patrizio and Giorgi, Daniela and Melzi, Simone and Rodolà, Emanuele},
            title = {{Straightedge and Compass Constructions on Surfaces}},
            author = {Mancinelli, Claudio and Puppo, Enrico},
            year = {2021},
            publisher = {The Eurographics Association},
            ISSN = {2617-4855},
            ISBN = {978-3-03868-165-6},
            DOI = {10.2312/stag.20211469}
            }