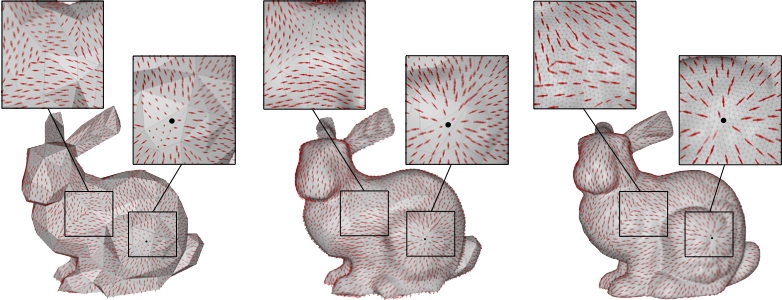
Estimating the differential properties of a signal sampled on a surface is of paramount importance in many fields of applied sciences. In the common practice, the surface is discretized with a polygonal mesh, the signal is sampled at its vertices and extended linearly over the triangles. This means that the polyhedral metric is assumed over the surface; the first derivatives of the signal become discontinuous across edges; and the second derivatives vanish. We present a new method based on surface fitting, which efficiently estimates the metric tensor, and the first and second order Riemannian differential operators at any point on the surface. All our differential operators are smooth within each triangle and continuous across the edges, providing a much better estimate of differential quantities on the - yet unknown - underlying smooth manifold.

(paper)

          @inproceedings {MP:2022,
            booktitle = {Smart Tools and Applications in Graphics - Eurographics Italian Chapter Conference},
            editor = {Cabiddu, Daniela and Schneider, Teseo and Allegra, Dario and Catalano, Chiara Eva and Cherchi, Gianmarco and Scateni, Riccardo},
            title = {{Nearly Smooth Differential Operators on Surface Meshes}},
            author = {Mancinelli, Claudio and Puppo, Enrico},
            year = {2022},
            publisher = {The Eurographics Association},
            ISSN = {2617-4855},
            ISBN = {978-3-03868-191-5},
            DOI = {10.2312/stag.20221255}
            }